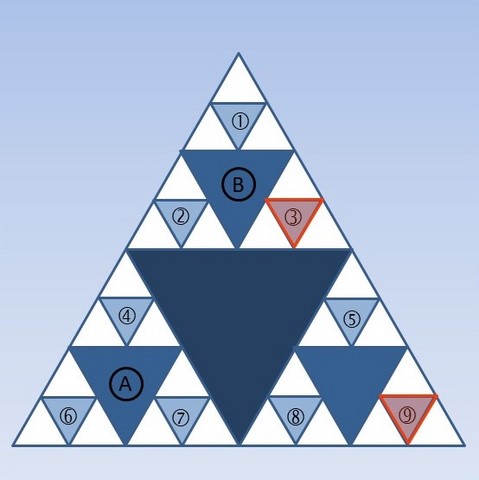
Pyramide de Sierpinski
Episode 3 : Triangle de Sierpinski et introduction aux translations
Des frises aux translations
Profitons d'une séance en demi-classe pour corriger le devoir à la maison (cf épisode 2) et faire un atelier sur les transformations en lien avec le triangle de Sierpinski.
Cet atelier a commencé par un petit travail sur les frises :
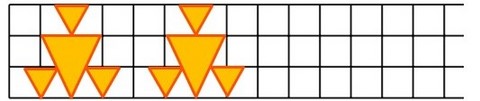
"La 1re figure possède-t-elle un axe de symétrie ? un centre de symétrie ? Décrire un procédé simple permettant de la réaliser à partir d'un seul motif. Réaliser les deux autres compositions."
Ce travail ludique et facile permet d'introduire progressivement les notions de translation et de frise, avec en fond des motifs élémentaires du triangle de Sierpinski.
Figure n°1

Figure n°2
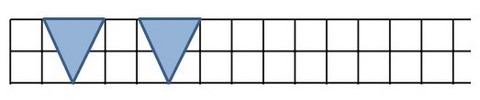
Figure n°3
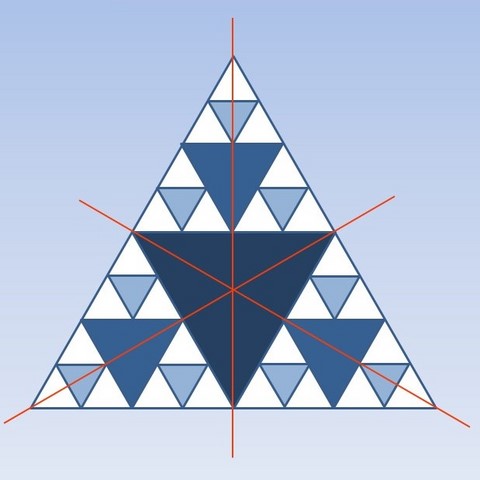
Symétries axiales et triangle de Sierpinski
Un triangle de Sierpinski a-t-il des axes de symétrie ? Si oui, lesquels ?
Symétrie centrale et triangle de Sierpinski
Un triangle de Sierpinski a-t-il un centre de symétrie ? (Et non !)

Et avec un papier calque !
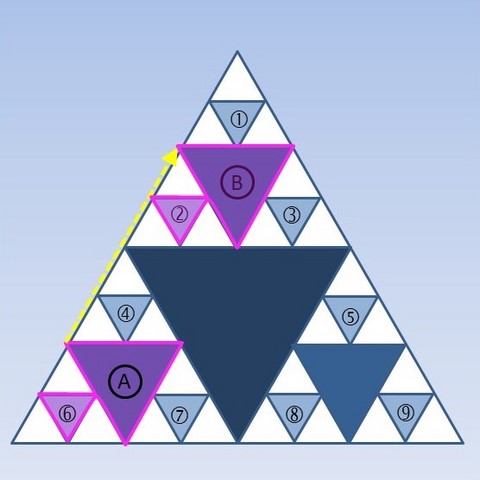
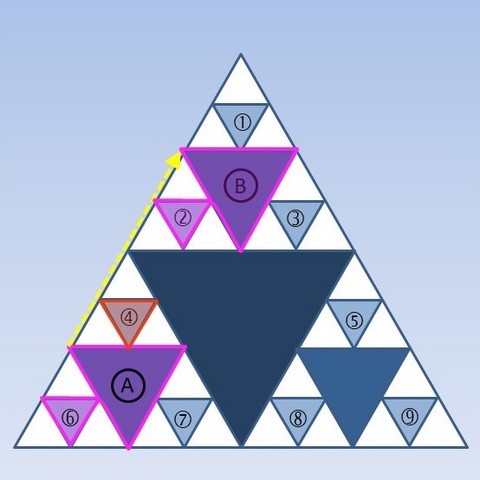
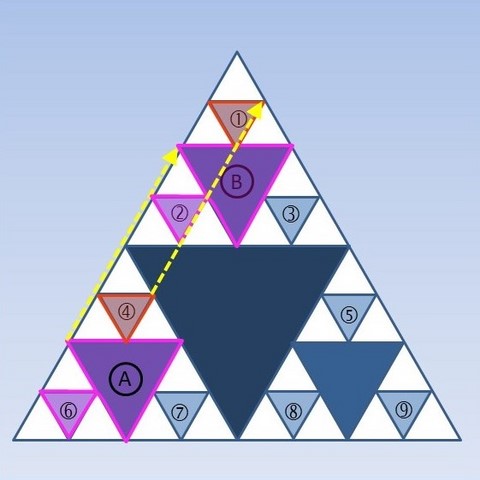
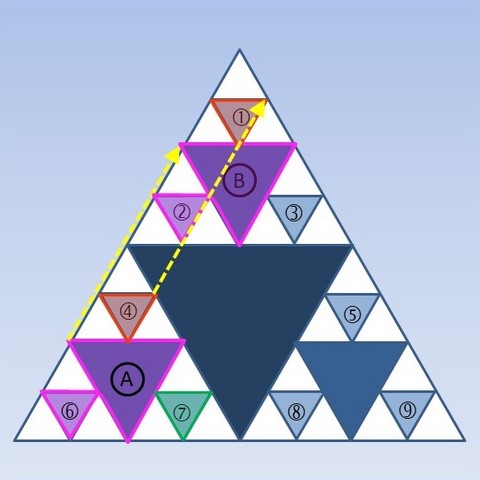
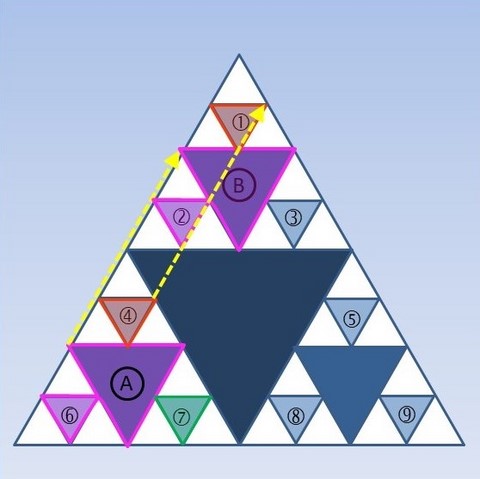
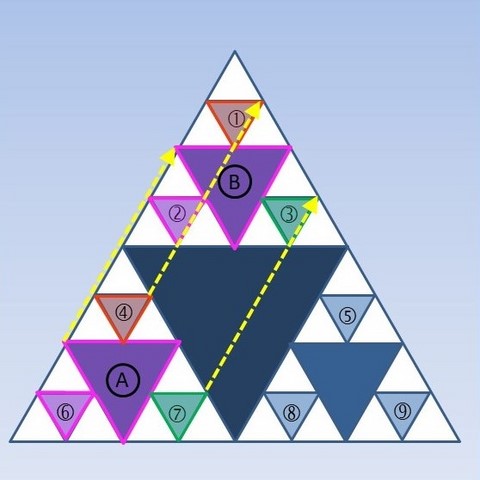
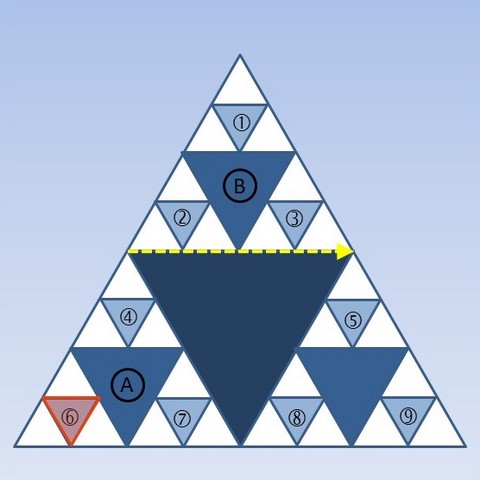
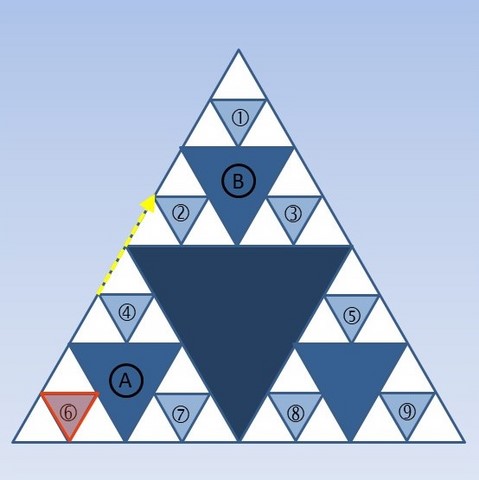
Après avoir décalqué les motifs A et 6, les déplacer le plus simplement possible pour que le triangle A vienne se superposer au triangle B. Où vient se superposer le triangle 6 ? Appliquer le même déplacement aux triangles 7 et 4.
Et dans d'autres directions ?
Mais encore...
Lors de cette partie, des remarques et des questions ont été soulevées avec pertinence et intérêt permettant d'approfondir les notions et de les prolonger à court ou moyen terme.
Parmi les commentaires, on retiendra tout d'abord, celui d'une élève qui a constaté qu'à partir du papier calque, on pouvait obtenir d'autres motifs en faisant d'autres "mouvements" : tout simplement en tournant ! Bonne remarque que l'on garde au chaud pour un prochain chapitre.
Ensuite, une différence a été mise en évidence entre la symétrie axiale et la translation : dans le triangle de Sierpinski, par symétrie axiale, on peut définir le symétrique de chacun des motifs, mais avec une translation dans cette figure, tous les motifs n'ont pas forcément une image (ou bien on va la construire en dehors du triangle).
Cette distinction a permis de prolonger et d'aborder un autre exemple celui des "Poissons et oiseaux" de M.C. Escher bien connu (ces deux configurations permettront plus tard de voir des exemples et contre-exemples de pavages).
Suite au prochain épisode !

<<< Episode 2 | Récapitulatif | Episode 4 >>>