Pyramide de Sierpinski Episode 2 : découverte des fractales et du triangle de Sierpinski
Lancement du projet
C'est parti ! La première étape de ce projet est enclenchée avec le devoir à la maison n°1 qui vise trois objectifs :
1- chercher ce qu'est une fractale et trouver quelques exemples autour de nous ;
2- construire une fractale mathématique : le triangle de Sierpinski ;
3- effectuer des mesures pour formuler des conjectures (Géom1) sur les triangles (anticipation Géom3) et dénombrer les triangles à des étapes bien précises (anticipation Calc4 et Calc7)
Un premier épisode pour découvrir le triangle de Mandelbrot et Sierpinski
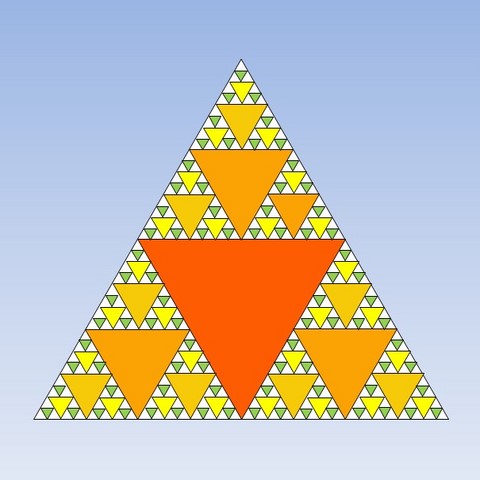
Avant de s'attaquer à la pyramide (géométrie dans l'espace), l'idée est de passer un peu de temps à étudier ce qui se passe dans le plan en particulier dans un triangle bien particulier, cher au mathématicien franco-américain Benoit Mandelbrot (1924-2010). Ce dernier a été l’inventeur des fractales, c'est-à-dire des courbes « infiniment morcelées » de telle manière qu'en zoomant sur une partie de la figure, on puisse trouver toute la figure.
Benoit Mandelbrot est aussi celui qui a fait connaître le triangle ci-contre au mathématicien polonais Waclaw Sierpinski (1882-1969).
C'est ce triangle qui nous intéresse ici sur cette première mission des 4es.
Exemple de fractale à l'état naturel
Le chou romanesco
Exemple de fractale géométrique
Triangle de Mandelbrot et Sierpinski
Exemple de fractale artistique
Jaméos Del Agua (Lanzarote)
Un premier épisode pour libérer ses talents artistiques
Voici un extrait des productions d'élèves qui n'est pas sans rappeler la devanture du Grand Musée Egyptien dont l'ouverture est prévue en 2018... ou 2019.
Un premier épisode pour semer des petites graines
La suite du devoir a proposé aux élèves de faire des mesures d'angles et de longueurs afin de formuler deux conjectures (Chapitre Géom1). Nous reviendrons dessus dans quelques semaines pour les démontrer grâce aux nouvelles connaissances du chapitre Géom3.
Une dernière question cherchait à dénombrer les nombres de triangles à différentes étapes. La priorité était de chercher, élaborer et communiquer une méthode permettant de déterminer la réponse le plus simplement et le plus rapidement possible. La formulation n'est pas tellement compliquée mais il a été mis en évidence quelques contraintes que deux prochaines notions (à découvrir dans les chapitres Calc4 et Calc7) nous permettront de simplifier.
Suspense ! La suite au prochain épisode !